Calculating the meteorological true wind from a moving vessel requires the observed wind to be adjusted for the mean horizontal motion of the ship. For example, consider a woman facing forward on the bow of a stationary ship on a calm day. If the ship begins moving forward, the woman will feel a fresh wind (the apparent wind) on her face. The wind induced by the ship's motion (M) must be removed from the apparent wind (A) to compute a meteorological true wind (T)
The apparent wind is calculated by adding the heading and zero reference angle to the platform-relative wind direction, thereby orienting the wind measured on the vessel to true north. The motion-induced wind has the same magnitude as the course vector (C) with the opposite sign
Note that C is the vector motion of the ship over the fixed Earth (i.e., direction equals COG, magnitude equals SOG). From (1), a true wind results by adding the course vector to the apparent wind vector
In the example above, the breeze felt by the woman on the bow would be canceled by the vector addition of the forward motion of the vessel.
The computation of a true wind is often misinterpreted as removing the
ship's course vector from the apparent wind vector. This error causes a
distinct stair-step pattern (Fig. 1) in the incorrectly calculated true wind speed (red) that is associated
with the ship's forward speed (black). In this case, the incorrectly calculated true wind speed
differs from a correctly calculated true wind speed (green) by up to 8 m
s-1 when the vessel is
moving at speeds greater than 2 m s-1. Similar stair-step patterns occur in true wind data when
other 180° errors are recorded in the platform-relative wind data (e.g., failure to report
an oceanographic convention or a wind vane installed with the zero reference toward the stern).
In general, a 180° error yields wind speeds that differ from the correct true wind speed by less than or equal to double the ship's speed.
The computation of meteorological true winds using an automated system
requires that the vector equations be broken down into components. A
detailed methodology is presented in appendix A.
Appendix B contains techniques to convert between meteorological, oceanographic, and Merchant Marine conventions.
b. Requirements for practical application
In many applications, from flux calculations to data ingestion in a
general circulation model, it is necessary to have more information than
the true wind speed and direction. For example, many applications require
that the wind speed be adjusted to the meteorological standard height of 10
m above the surface. Other applications require winds relative to the
surface current (e.g., scatterometry, stresses, forcing of ocean models),
while meteorological forecasts require earth-relative winds. The calculation of surface fluxes (of momentum, sensible heat, and latent heat) and atmospheric stability require additional observations including the air temperature, the skin temperature of the water (approximated by the near surface temperature), and a measure of the humidity (Liu et al. 1979). Observations of pressure are also useful to convert typical humidity measurements to specific humidity, which is used in height corrections and flux calculations.
In recent years, the influence of sea state on fluxes and drag
coefficients has become of interest (Smith et al. 1992; Donelan et al.
1997; Bourassa et al. 1998). There is some controversy regarding the dependence on sea state. Several flux parameterizations require wave age or the phase speed of the dominant waves (e.g., Smith et al. 1992; Bourassa et al. 1998). Recently, the direction of the wind relative to the direction of wave propagation has been shown to have a large impact on the surface stress and drag coefficients (Donelan et al. 1997; Bourassa et al. 1998).
Essential metadata, such as the height of the sensors, should be recorded for use in
height adjustment and the calculation of fluxes. In theory, the height of the temperature
and humidity measurements must be the same, but these can differ from the height of the
anemometer (Liu et al. 1979). In practice, the height of the temperature and humidity
observations has little influence on the height adjustment of winds; however, these
heights can have a serious impact on the calculation of fluxes (e.g., stress and latent
heat). In most cases, the lack of metadata prevents the accurate calculation of surface
fluxes. One of the most common errors in ten-meter wind speed is due to incorrect
specification of anemometer heights. In several cases this height was given relative to
the deck rather than relative to the water surface (since the waterline of vessels
changes with the load, this error is understandable). Ideally, data records would include
the height of the deck above sea level; however, such information is available from only
very few highly specialized research vessels.
4. Evaluating the quality of wind data
Our experience has shown that missing data due to instrument
malfunctions, encoding errors, approximations, and oversights are common
occurrences in automated data. Techniques to retrieve useful true wind
information from these data sets are discussed in section
5. Application of quality control procedures to identify problems is an
essential first step. In this section, quality control methods discussed
include automated and visual inspections for erroneous data values and the
identification of errors due to a vessel's acceleration. A brief note is
included concerning the unavoidable problem of flow distortion. After
identifying problems with wind and navigation data, techniques for
estimating true wind (section 5) can be applied to incomplete data sets.
a. Identifying erroneous values
WOCE-MET utilizes a two-step process to quality control both true wind data and the
variables necessary to calculate a true wind (Smith et al. 1996). The first step is
automated and identifies erroneous ship positions and physically unrealistic observations.
A position check verifies that the latitude and longitude values are over water, while a
speed check verifies that the vessel has not moved forward at a rate greater than 15 m
s-1. A range check of realistic wind directions (0 to 360°) and wind speeds (< 40 m s-1) is also performed. This latter check may highlight realistic extreme winds; thus, WOCE-MET personnel visually verify all flags added by the automated quality control.
Visual inspection of the data, though time consuming, is essential. The analyst adds flags for spikes, known instrument malfunctions, discontinuities, and values that are highly inconsistent with the surrounding trend. This latter contingency requires knowledge of the behavior of wind data from vessels and is subjective. Automated tests for discontinuities and spikes are available (Vickers and Mahrt 1997), but we find visual inspection to be adequate. Based on 82 ship months of automated meteorological true winds, the two-level quality control applies flags to an average of 5% of wind speeds and 6% of wind directions. On some vessels, the visual inspection determines that all true wind directions and speeds are incorrect. Removing or correcting these flagged true wind values is essential before performing any application using the data.
The two-level quality control employed by WOCE-MET has proven invaluable. For two of
the four vessels reporting all values necessary to compute true winds, the visual
inspection allowed the analyst to determine that the platform wind direction was reported
opposite the desired meteorological direction. When problems of this type are located, the
platform wind is corrected and new meteorological true winds are calculated. The impact of
fixing 180° errors is evident (Table 2) when the true wind values are compared to
independent wind measurements from the NASA Scatterometer (NSCAT; Bourassa et al. 1997).
Table 2 reveals that the correction of the 180° error decreased the root-mean-square (rms) difference between collocated (within 25 km and 20 minutes) NSCAT and ship winds by 44% for speed and 33% for direction. The correlation coefficient for collocated wind speed improves by 74%. Visual inspection of the wind data is necessary and in some cases leads to a much larger set of useable wind values.
b. Averaging techniques and acceleration problems
The choice of averaging techniques impacts the accuracy of true winds. Ideally, observations (platform relative winds) would be made over short intervals and used to calculate true winds corresponding to those times. The true winds would then be averaged and stored. At this time observational equipment and data processing are equal to the task (e.g., the TAO buoy array; Hayes et al. 1991); however, this ideal is rarely achieved.
The averaging time for platform relative winds should be sufficiently short that
navigational and ship-relative wind observations are approximately constant. The size of
averaging periods depends on accuracy requirements and operational constraints for the
vessel. For example, research vessels spend a relatively large fraction of their operating
time accelerating or decelerating. It will be shown that these changes in velocity can be
identified in one minute averages; therefore, shorter averaging times (perhaps <10
seconds) are recommended for the navigational parameters and platform relative winds. The
requirements for storage and post processing could be copious; therefore, we recommend
that this averaging be processed by the shipboard instruments, and an average of the true
winds (over 15-300 seconds) be recorded. A further advantage of averaging true winds as
vectors, rather than speeds and directions, is the elimination of problems with the
360-0° breakpoint. At this time, such procedures are rarely implemented.
Typically, platform-relative winds and navigational parameters utilized in the true
wind calculations (section 3a and appendix A) are averaged over intervals ranging from one
minute to an hour. Since the true wind equations are nonlinear, they are accurate only
when all the input parameters are approximately constant over the averaging period. When
appropriate averaging cannot be applied, and the observations are too variable, the true
winds should be flagged as suspect. One noticeable and regular manifestation of this
problem occurs when research vessels accelerate or decelerate. The impact of changing ship
velocities is examined for an Improved METeorology (IMET) system (Hosom et al. 1995) on
the R/V Knorr, which records platform-relative winds in one minute intervals. These
acceleration errors manifest themselves as spikes in the true wind speed and direction
data (Fig. 2). The magnitude of the error in individual calculations is dependent on the
rate of acceleration; however, for the R/V Knorr the spikes can approach 2 m s-1
and 60°.
We have found, empirically, that quality control criteria can be based on the standard
deviation of the ship's velocity ( V) determined from one minute observations within a longer averaging period (six minutes in the following example):
V) determined from one minute observations within a longer averaging period (six minutes in the following example):
 | (4) |
where N is the number of observations and the overbar indicates averages of these N
observations. For many applications the uncertainty due to acceleration is relatively small and can
be ignored. However, satellite measurements of the near surface winds by NSCAT are sufficiently
accurate (Bourassa et al. 1997) that this additional uncertainty is apparent when comparing
ship-based winds to remotely sensed winds. The impact of this criterion is shown in the mean and rms
differences between winds from NSCAT and the R/V Knorr. Without this criterion, there are 18
collocations (closest observations within 25 km and 20 minutes) with a mean difference (satellite
minus ship) of -0.8 m s-1, and a rms difference of 2.0 m s-1. When observations with  v > 1.0 m s-1 (12 collocations with accelerations that are considered too rapid and prolonged) are flagged and removed, the mean difference changes to 0.55 m s-1, and the rms difference drops to 1.3 m s-1. These findings are consistent with an assessment of the NSCAT-1 model function in comparisons with the NDBC buoys by M. Freilich and R. S. Dunbar (1997, personal communication) and the TAO buoys by K. Kelly (1997, personal communication). The change in the mean is statistically significant, corresponding to 4.3 standard deviations of the mean. The almost 50% overestimation of the rms difference, prior to this quality control criterion, shows that there are applications where changes in the vessel's velocity can result is substantial averaging-related errors in the calculated true winds.
v > 1.0 m s-1 (12 collocations with accelerations that are considered too rapid and prolonged) are flagged and removed, the mean difference changes to 0.55 m s-1, and the rms difference drops to 1.3 m s-1. These findings are consistent with an assessment of the NSCAT-1 model function in comparisons with the NDBC buoys by M. Freilich and R. S. Dunbar (1997, personal communication) and the TAO buoys by K. Kelly (1997, personal communication). The change in the mean is statistically significant, corresponding to 4.3 standard deviations of the mean. The almost 50% overestimation of the rms difference, prior to this quality control criterion, shows that there are applications where changes in the vessel's velocity can result is substantial averaging-related errors in the calculated true winds.
c. Flow distortion
Another problem that occurs with ship based winds is flow distortion. Structures (i.e., the entire ship, and to a lesser extent the measuring device) cause air to deviate from the path it would take if the structures were not present. Flow distortion occurs in the wake of structures, around structures, and upwind of structures. The resulting change in wind characteristics (speed, direction, and the variation of these quantities) is highly dependent on shape of the vessel, instrument position, and wind direction relative to the vessel's heading. Recently, computational fluid dynamics has been successfully applied to correct for the impacts of flow distortion (Yelland et al. 1998). Other techniques are relatively simple, however, they are much more crude. The range of directions, over which the influence of flow distortion is a relatively strong function of platform-relative wind direction, can be estimated by binning the wind speed as a function of this direction (Thiebaux 1990). We have found a similar result with the variation in the wind speed. However, neither of these approaches indicates the impact of the flow distortion nor the angles at which the impact is a minimum. These techniques can only be used to isolate angles at which the impact of flow distortion is approximately constant, which can be advantageous for data analysis.
5. Estimating true winds from incomplete data
Incomplete observations from 16 of 20 studied vessels left only four with all values
required to calculate meteorological true winds (Table 3).
Consequently, we investigated methods for estimating meteorological true winds when some
of the navigation parameters are missing. The two most common occurrences of missing
navigation data are vessels reporting only a COG and SOG (no heading) or a heading and
SOWFA (no COG; Table 3 ). In these cases, if the platform-relative winds and zero reference angle are known, estimates for the true winds can be made; however, the underlying assumptions can lead to serious errors. Empirical studies reveal the conditions under which these estimations are practical.
If the heading is missing, a true wind can be estimated by replacing the heading with
the COG. This estimate is hereafter called a course-estimated wind. Thus, the apparent
wind direction is calculated by summing the COG angle, zero reference angle, and
platform-relative wind direction. The accuracy of this estimate is questionable at low
ship speeds where the course-estimated wind direction (black, Fig. 3a) deviates wildly from the actual true wind (red).
The range of SOG where the course-estimated winds are valid can be determined
empirically and depends upon the vessel and its region of operation. As an example, we
determine this range using two vessels that reported all necessary values to WOCE-MET.
Differences between the course-estimated and true wind direction are computed using
quality controlled observations from the R/V Thompson (8.9 months) and the R/V
Knorr (4.7 months). The direction differences are separated into 0.5 m s-1 SOG
bins and a rms difference is calculated for each bin. Rms differences and the number of
values in each SOG bin, from 0 to 9 m s-1, are presented for the R/V Thompson and
R/V Knorr (Figure 4). For low ship speeds (SOG < 2 m s-1),
both vessels exhibit rms difference near or greater than 60°. Direction differences
drop below 20° when the SOG exceeds 2.5 m s-1 for the Thompson and 4.0 m s-1
for the Knorr. Determining a threshold SOG for which the rms difference is within
an acceptable range is user dependent. For a rms wind direction difference less than
10°, the threshold SOG is 3.5 m s-1 for the Thompson and 5 m s-1 for the
Knorr (Fig. 4) . In summary, the primary
limitation of the course-corrected wind estimates is that they are sensitive to the SOG; becoming unreliable at low ship speeds.
Inaccuracies in the course-estimated winds are directly related to measuring only
SOG and COG without a heading. Eight of twenty studied vessels relied solely on single
receiver GPS systems to measure their geographical position and to provide values of SOG
and COG. A single receiver GPS is not designed to measure heading; therefore, it cannot
always estimate the heading with sufficient accuracy. This problem is exaggerated at low
ship speeds when current and wind forces on the ship can cause large differences between
heading and COG (Fig. 3b,c). As a result, the true winds reported by these eight vessels are course-estimated winds. Furthermore, errors in course-estimated winds are increased if the latitude and longitude are not recorded to at least the thousands decimal place. The ability to measure the orientation of the vessel using only GPS technology can be improved using a multiple receiver GPS, but for vessels with single receiver GPS we recommend the addition of a gyrocompass to record the heading.
When a vessel relies on navigation without the aid of technology referenced to the fixed Earth, it is common practice to measure only the heading of the vessel and the SOWFA. When only heading and SOWFA are measured, an Earth-relative wind cannot be computed. Instead, an estimate referenced to the water can be created by replacing the course vector in (3) with a heading vector, H, where the |H| equals SOWFA and the direction of H is the direction the bow is pointing (referenced to true north). Unlike the course-estimated winds, frequency diagrams (not shown) of this heading-estimated wind minus the meteorological true wind reveal differences with no dependence on forward ship speed. Instead, the heading
estimated wind deviates from a true wind only when the SOWFA and SOG are different from one another.
A time series plot for 12 hours of wind data from the R/V Knorr illustrates the differences
that can occur (Fig. 5). In this case a 2 m s-1 difference in the
SOWFA and SOG (Fig. 5b) results in
an average direction error of 25° (Fig. 5a). Variations between the SOWFA and SOG are related to currents.
In summary, an examination of a total of 13.6 ship months of automated observations from
two vessels shows that, when computation of a meteorological true wind is not possible,
heading-estimated winds are superior to course-estimated winds. The accuracy of the
heading-estimated winds is limited by the difference between SOWFA and SOG. When these speeds
are not significantly different, the heading-estimated and true wind directions are nearly
identical. When an operator only records the SOG and COG, the potentially large differences
between the COG and heading, at low ship speeds, result in large differences between
course-corrected and true winds.
6. Summary and recommendations
Problems in computing true winds from automated systems have been identified and solutions are demonstrated. Principle problems include confusion related to inconsistencies in definitions for true wind used by meteorologists, oceanographers, and the Merchant Marine, and the lack of standard reporting of both wind and navigation measurements (or the convention used). The primary recommendation is setting a standard for reporting the six values needed to compute a true wind: COG, SOG, heading, zero reference, and platform-relative wind direction and speed. Additional metadata, especially the height of the wind sensor relative to the water surface, must also be reported.
Accurate meteorological true winds result from the vector sum of the
ship's motion relative to the fixed Earth and the apparent wind. Details of
this calculation are outlined in appendix A.
Conversions from the meteorological true wind to oceanographic and Merchant
Marine definitions are detailed in appendix B.
The true wind calculations and conversions presented can be applied to AWS
and non-automated wind measurements.
True winds must be quality controlled before application to identify errors. At WOCE-MET, a two-level quality control system comprised of an automated preprocessor and a detailed visual examination has proven effective in identifying both minor (e.g., out of range values, spikes, ship acceleration) and major (e.g., incorrectly oriented platform-relative wind) errors.
When dealing with incomplete data sets (e.g., approximately 80% of examined AWS data), true winds can be estimated within determinable limitations. A better estimate for a wide range of forward ship speeds can be obtained when a heading and SOWFA are measured, rather than an estimate derived from SOG and COG when no heading is available. The heading-estimated wind varies from a true wind only when the SOWFA and SOG are significantly different. The uncertainty in course-estimated winds has a strong dependency on the forward ship speed. Empirical studies show course-estimated wind directions to be unreliable (rms > 60°) when the SOG < 2.0 m s-1. Useful estimates can be obtained at higher ship speeds; however, the threshold SOG depends upon the ship, the vessel's operating area, and the users desired level of uncertainty.
The following recommendations are made for future automated observing systems, thereby avoiding the need to estimate the true winds. The standard set of measurements needed to compute a true wind (i.e., SOG, COG, heading, wind relative to the vessel) must all be logged at the same frequency as the standard meteorological variables. Averaging should be applied to true winds calculated from shorter term (0.5 to 10 sec.) observations. Essential metadata (e.g., zero reference, instrument heights) must be reported. When it is essential that measurements be collected without losing data, redundancy should be planned for both the navigation and wind measurements. When an instrument fails in a redundant system, alternate measurements can be used in the computation of true wind or an estimate of the true wind can be created. For example, 3 years of AWS wind data on one studied vessel were lost due to the failure of a navigational compass in the wind sensor. If the ship's gyrocompass heading had been archived in the meteorological data stream, the loss could have been avoided. If the marine community utilizes the techniques and recommendations herein, a superior quality of high temporal resolution true wind observations can be computed from automated platforms on vessels at sea.
Acknowledgments: The authors wish to thank Dr. Leslie Hartten for her comments on ship wind measurements, Ms. Masha A. Medvedeva for her contributions to the wind analysis, and the anonymous reviewers for their constructive comments. The authors also acknowledge the professional support of Dr. David M. Legler. We further express our gratitude to the personnel both at sea and on shore that provided the data for this study.
COAPS receives its base funding from the Physical Oceanography Section
of the Office of Naval Research. WOCE-MET and this research are funded by
the Physical Oceanography Section of the National Science Foundation, grant
OCE-314515, and from the NASA JPL NSCAT Project, contracts 957649 and 980646.
Appendix A
Details for Automated Calculation of True Winds
This appendix is a tutorial containing algorithms for calculating meteorological
true winds from ship observations. The mathematics and all necessary variables (Table
A1) are discussed and an example provided.
All calculations are performed in the mathematical coordinate system which has an
angle of zero degrees on the positive x-axis with angles increasing in a
counterclockwise direction. Each vector direction, originally defined using the
meteorological conventions (Table 1), is converted to mathematical
coordinates prior to other calculations (see Table B1 to convert from other conventions). Primes (') denote values in math coordinates.
Platform-relative winds (P) and navigational data are used to calculate apparent (A) and true (T) winds. The direction of the apparent wind in the math coordinates is
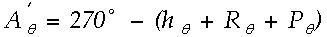 | (A1) |
where h is the vessel's heading, R is the zero reference, and the
subscript  designates an angle. The magnitude of A
is the same as the magnitude of P. Use of the heading instead of the
COG in (A1) is essential because the bow is rarely oriented in the direction of
ship motion over the fixed Earth. As an example, consider the bow of a ship is
oriented directly to the east (
designates an angle. The magnitude of A
is the same as the magnitude of P. Use of the heading instead of the
COG in (A1) is essential because the bow is rarely oriented in the direction of
ship motion over the fixed Earth. As an example, consider the bow of a ship is
oriented directly to the east ( = 90°). If there is either a strong current or wind from the north, then the vessel will be pushed to the south, resulting in a COG greater than 90°.
= 90°). If there is either a strong current or wind from the north, then the vessel will be pushed to the south, resulting in a COG greater than 90°.
Most ships utilize the bow as the zero reference for the platform-relative wind, but
there are exceptions to this practice. When another point on the ship is used as a zero
reference for the wind vane, the angle between this reference and the bow
(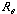 in Fig. A1) must be included in (A1) to correctly calculate the apparent wind direction.
in Fig. A1) must be included in (A1) to correctly calculate the apparent wind direction.
The COG of the vessel ( ) in math coordinates is
) in math coordinates is
 | (A2) |
The true wind is then computed by summing the vector components of the apparent wind and ship motion:
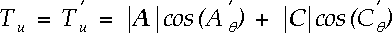 | (A3a) |
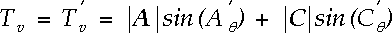 | (A3b) |
where positive Tu and Tv are the eastwards and northwards
components of the true wind in the Earth reference frame. The true wind speed
( T
T ) and direction (
) and direction ( ) can then be calculated:
) can then be calculated:
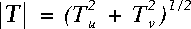 | (A4) |
and
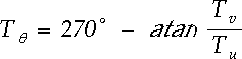 | (A5) |
The 270° in (A5) converts the value of  to a direction from which the wind is blowing (meteorological convention) in the Earth coordinate system. For (A5) to return a correct angle, the atan function must have a range from -180° to 180° to determine the vector's trigonometric quadrant (e.g., the FORTRAN atan2 function). Also, any program using (A5) must have a check to avoid dividing by zero.
to a direction from which the wind is blowing (meteorological convention) in the Earth coordinate system. For (A5) to return a correct angle, the atan function must have a range from -180° to 180° to determine the vector's trigonometric quadrant (e.g., the FORTRAN atan2 function). Also, any program using (A5) must have a check to avoid dividing by zero.
As an example calculation consider a ship (Fig. A2) with a heading
( ) of 30.0° and a COG (
) of 30.0° and a COG ( ) of 45.0° both referenced to true north (0° in
a fixed Earth reference frame). The vessel is travelling at a SOG (
) of 45.0° both referenced to true north (0° in
a fixed Earth reference frame). The vessel is travelling at a SOG ( C
C ) of 5.0 m
s-1. The platform-relative wind, with the bow as the zero reference angle (
) of 5.0 m
s-1. The platform-relative wind, with the bow as the zero reference angle (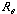 = 0.0°), is blowing from a direction (
= 0.0°), is blowing from a direction ( ) of 250.0° with a magnitude (
) of 250.0° with a magnitude ( P
P ) of 10.0 m s-1. The
conversion to math coordinates using (A1) and (A2) results in
) of 10.0 m s-1. The
conversion to math coordinates using (A1) and (A2) results in  = 350.0° and
= 350.0° and  =
45.0°. Computing the true wind components using (A3a) and (A3b) gives a
Tu = 13.4 m s-1 and a Tv = 1.8 m s-1. The meteorological true wind speed from (A4) is 13.5 m s-1 and the true wind direction, (A5), is blowing from 262.3°.
=
45.0°. Computing the true wind components using (A3a) and (A3b) gives a
Tu = 13.4 m s-1 and a Tv = 1.8 m s-1. The meteorological true wind speed from (A4) is 13.5 m s-1 and the true wind direction, (A5), is blowing from 262.3°.
Table A2 provides sample input and the output that should be returned
from a meteorological (and 1st Merchant Marine) true wind algorithm. Any
algorithm used to calculate true winds should duplicate these results.
FORTRAN, C, and IDL (Interactive Data Language) routines for computing
meteorological true winds are available at the URL:
coaps.fsu.edu/WOCE.
Appendix B
Conversions between Different Conventions
As previously stated, the meteorological, oceanographic, and Merchant
Marine conventions are different when defining true wind vectors. In the
meteorological convention, wind direction is defined as the direction
from which the wind is blowing in the Earth reference frame. The
Merchant Marine has an identical convention, but they also define a true wind
with a direction referenced to the bow of the ship. In the oceanographic
convention, wind direction is defined with a direction toward which
the wind is blowing. This confusion presents problems when using true wind
data. Table B1 provides the conversions between each of the conventions.
After all direction conversions, the modulus of the returned value must be
taken with respect to 360° to ensure a direction between 0° and
360°.
References
- Bourassa, M. A., M. H. Freilich, D. M. Legler, W. T. Liu, and J. J. O'Brien, 1997: Wind observations from new satellite and research vessels agree. EOS Trans. Amer. Geophys. Union, 78(51), 597, 602.
- Bourassa, M. A., D. G. Vincent, W. L. Wood, 1998: A flux parameterization including the effects of capillary waves and sea state. J. Atmos. Sci., accepted.
- Bowditch, N., 1984: American Practical Navigator: An Epitome of Navigation. DMA Stock No. NVPUB9V1, LC no. VK555.A48, Defense Mapping Agency, Washington, D.C., 1414 pp.
- Donelan, M. A., W. M. Drennab, and K. B. Kataros, 1997: The air-sea momentum flux in conditions of wind sea and swell. J. Phys. Oceanogr., 27, 2087 - 2099.
- Fritschen, L.J., and L.W. Gay, 1979: Environmental Instrumentation.
Springer-Verlag, 216 pp.
- Hartten, L.M., 1998: Reconciliation of surface and profiler winds at ISS sites. J. Atmos. Oceanic Technol., 15, 826-834.
- Hayes, S.P., L.J. Mangum, J. Picaut, A. Sumi, and K. Takeuchi (1991): TOGA-TAO: A moored array for real-time measurements in the Tropical Pacific Ocean. Bull. Amer. Meteor. Soc., 72, 339-347.
- Hosom, D.S., R.A. Weller, R.E. Payne, and K.E. Prada, 1995: The IMET (Improved Meteorology) ship and buoy systems. J. Atmos. Oceanic Technol., 12, 527-540.
- Huschke, R.E. (ed.), 1959: Glossary of Meteorology. American Meteorological Society, 638 pp.
- Kahma, K.K., and M. Leppäranta, 1981: On errors in wind speed observations on R/V Aranda. Geophysica, 17, 155-165.
- Kent, E.C., P.K. Taylor, B.S. Truscott, and J.S. Hopkins, 1993: The accuracy of Voluntary Observing Ships' meteorological observations - results of the VSOP-NA. J. Atmos. Oceanic Technol., 10, 591-608.
- Liu, W. T., K. B. Katsaros, and J. A. Businger, 1979: Bulk parameterization of air-sea exchanges of heat and water vapor including the molecular constraints at the interface. J. Atmos. Sci., 36, 1722 - 1735.
- Pierson, W.J., Jr., 1990: Examples of, reasons for, and consequences of the poor quality of wind data for the marine boundary layer: Implications for remote sensing. J. Geophys. Res., 95, 13313-13340.
- Rahmstorf, S., 1989: Improving the accuracy of wind speed observations from ships. Deep-Sea Res., 36, 1267-1276.
- Smith, S. D., R. J. Anderson, W. A. Oost, C. Kraan, N. Maat, J. DeCosmo, K. B. Katsaros, K. L. Davidson, K. Bumke, L. Hasse, and H. M. Cadwick, 1992: Sea surface wind stress and drag coefficients: the HEXOS results. Bound.-Layer Meteorol., 60, 109-142.
- Smith, S.R., C. Harvey, and D.M. Legler, 1996: Handbook of quality control procedures and methods for surface meteorology data. WOCE Report 141/96, COAPS Report 96-1, WOCE Data Assembly Center, COAPS, Florida State University, Tallahassee, Florida, 32310, USA, 56pp.
- Thiebaux, M. L., 1990: Wind tunnel experiments to determine correction functions for shipborne anemometers. Canadian Contractor Report of Hydrography and Ocean Sciences 36, Bedford Inst. Oceanography, Dartmouth, Nova Scotia, 57pp.
- Vickers, D. and L. Mahrt, 1997: Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Oceanic Technol., 14, 512-526.
- Wilkerson, J.C. and M.D. Earle, 1990: A study of differences between environmental reports by ships in the Voluntary Observing Program and measurements from NOAA buoys. J. Geophys. Res., 95(C3), 3373-3385.
- World Meteorological Organization, 1996: Guide to meteorological instruments and methods of observation. WMO - No. 8, Geneva, Switzerland.
- Yelland, M. J., B. I. Moat, P. K. Taylor, R. W. Pascal, J. Hutchings, and V. C. Cornell, 1998: Wind stress measurements from the open ocean corrected for airflow distortion by the ship. J. Phys. Oceanogr., 28, 1511-1526.
- Yelland, M. J., P. K. Taylor, I. E. Consterdine, and M. H. Smith, 1994: The use of the
inertial dissipation technique for shipboard wind stress determination. J. Atmos. Oceanic
Technol., 11, 1093 - 1108.
Tables
Table 1. Definitions of wind and navigation parameters for the three most common sources of observations. Differences from the meteorological conventions are emphasized with italics. The Merchant Marine has two definitions of apparent wind: (1) the wind experienced on the deck of the ship with a direction referenced to true north (consistent with the meteorological definition), and (2) the wind measured by the anemometer (similar to the meteorological platform-relative wind). The Merchant Marine also has two definitions for true wind: (1) relative to true north, and (2) relative to the bow of the ship. The use of a zero reference angle (zero ref. ang.) measured with respect to the bow is common to all three groups.
| Meteorological
Definitions | Velocity frame of
reference | Directional frame of
reference | Direction convention |
| Ship COG and SOG | fixed Earth | true north | moving to |
| Ship heading | fixed Earth | true north | moving to |
| Platform-relative winds | ship | zero ref. ang. | moving from |
| Apparent winds | ship | true north | moving from |
| True winds | fixed Earth | true north | moving from |
| | | |
| Oceanographic
Definitions | Velocity frame of
reference | Directional frame of
reference | Direction convention |
| Ship COG and SOG | fixed Earth | true north | moving to |
| Ship heading | fixed Earth | true north | moving to |
| Platform-relative winds | ship | zero ref. ang. | moving to |
| Apparent winds | ship | true north | moving to |
| True winds | fixed Earth | true north | moving to |
| | | |
| Merchant Marine
Definitions | Velocity frame of
reference | Directional frame of
reference | Direction convention |
| Ship COG and SOG | fixed Earth | true north | moving to |
| Ship heading | fixed Earth | true north | moving to |
| Platform-relative winds | ship | zero ref. ang. | moving from |
| Apparent winds (1) | ship | true north | moving from |
| Apparent winds (2) | ship | bow of ship | moving from |
| True winds (1) | fixed Earth | true north | moving from |
| True winds (2) | fixed Earth | bow of ship | moving from |
Table 2. Rms differences between collocated ship and NSCAT true winds for ship data with a 180° error in the platform wind and for the corrected true wind. Also presented is the improvement in the correlation coefficient for collocated wind speeds.
| True wind | Rms wind speed difference | Rms wind direction difference | Correlation coeff. for wind speed |
| with 180° error | 3.2 m
s-1 | 21° | 0.51 |
| Corrected | 1.8 m
s-1 | 14° | 0.89 |
| Percent change | -44% | -33% | 74% |
Table 3. Based on 20 vessels equip with automated wind systems, the number that report ( ) the parameters needed for computing a meteorological true wind or an estimate of the true wind (heading or course missing).
) the parameters needed for computing a meteorological true wind or an estimate of the true wind (heading or course missing).
Platform
Relative Wind |
Heading | Course
over Ground | Speed
over Ground | Speed
over
Water | Number
of ships Reporting |
 |  |  |  | - | 4 |
 | - |  |  | - | 8 |
 |  | - | - |  | 6 |
Table A1. Variables needed for true wind vector (T) calculation
Parameter |
Type |
Symbol | Direction
Reference
Frame | Velocity Reference Frame |
| Ship heading | scalar |  | true north | -- |
| Ship course over ground | vector | C | true north | fixed Earth |
Platform-relative wind
(direction from which wind is blowing) | vector | P | zero reference on ship | ship |
| Zero reference angle for platform-relative wind | scalar | 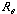 | bow of ship | -- |
Table A2. Sample input and output for the true wind calculation. For simplification, the zero
reference is the bow of the vessel (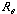 ) = 0°. The table is divided into input (not shaded) and output (gray shaded) values. Note that both the apparent and the true wind directions are referenced to true north, and all wind directions are angles from which the wind is blowing. Also the WMO convention is utilized for calm (direction = 0°) and north winds (direction = 360°).
) = 0°. The table is divided into input (not shaded) and output (gray shaded) values. Note that both the apparent and the true wind directions are referenced to true north, and all wind directions are angles from which the wind is blowing. Also the WMO convention is utilized for calm (direction = 0°) and north winds (direction = 360°).
Vessel Course
over the Ground
(deg.) | Vessel Speed over the Ground
(m s-1) | Vessel Heading (deg.) | Platform Wind Direction (deg) | Platform and | Apparent Wind Direction
(deg.) | True Wind Direction
(deg.) | True Wind Speed
(m s-1) |
Apparent Wind Speed
(m s-1) |
| 0.0 | 0.0 | 0.0 | 90.0 | 5.0 | 90.0 | 90.0 | 5.0 |
| 0.0 | 0.0 | 90.0 | 90.0 | 5.0 | 180.0 | 180.0 | 5.0 |
| 0.0 | 5.0 | 0.0 | 360.0 | 5.0 | 360.0 | 0.0 | 0.0 |
| 0.0 | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 180.0 | 5.0 |
| 180.0 | 5.0 | 180.0 | 180.0 | 5.0 | 360.0 | 360.0 | 10.0 |
| 90.0 | 5.0 | 90.0 | 90.0 | 5.0 | 180.0 | 225.0 | 7.1 |
| 90.0 | 5.0 | 45.0 | 135.0 | 5.0 | 180.0 | 225.0 | 7.1 |
| 225.0 | 5.0 | 225.0 | 270.0 | 5.0 | 135.0 | 90.0 | 7.1 |
| 270.0 | 3.0 | 270.0 | 90.0 | 4.0 | 360.0 | 36.9 | 5.0 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
Table B1: Conversion table to change between conventions for apparent and true wind
directions. Note that the Merchant Marine utilizes two definitions for apparent and true wind
(Table 1). The first Merchant Marine definitions are identical to those
used in meteorology and should be treated identically (Merchant Marine (1) = Meteorology)
when using this conversion table. The Merchant Marine listings in this table refer to the
second (2) apparent and true wind definitions from Table 1. After each direction conversion, a modulus with respect to 360° must be performed to ensure a value in the range of 0° to 360°.
| Given | Meteorology  Oceanography Oceanography | Oceanography  Meteorology Meteorology |
| Apparent Wind | Add 180° | Add 180° |
| True Wind | Add 180° | Add 180° |
| | |
| Given | Meteorology  Merchant Marine (2) Merchant Marine (2) | Merchant Marine (2)  Meteorology Meteorology |
| Apparent Wind | Subtract heading of ship | Add heading of ship |
| True Wind | Subtract heading of ship | Add heading of ship |
| | |
| Given | Merchant Marine (2)  Oceanography Oceanography | Oceanography  Merchant Marine (2) Merchant Marine (2) |
| Apparent Wind | Add heading of ship
and add 180° | Subtract heading of ship
and add 180° |
| True Wind | Add heading of ship
and add 180° | Subtract heading of ship
and add 180° |
Figures

Fig. 1. Example of accurate true wind calculation (green) vs. incorrect calculation (red) for the R/V Knorr. Note that both the platform-relative wind (blue) and the incorrect true wind have a signal of the ship's Earth-relative speed (black).

Fig. 2. Spikes that occur in true wind direction and speed caused by the acceleration of the vessel. Displayed are the true wind direction and speed, heading, and speed over the ground from the automated weather system on the R/V Knorr (0730 to 2359 UTC 19 August 1995).

Fig. 3. Time series plots of (a) course-estimated (black) vs. meteorological true (red) wind direction, (b) vessel course (black) vs. heading (red), and (c) vessel speed over the ground from the R/V Thompson (03 August 1993).

Fig. 4. Rms differences of course-estimated minus true wind direction (filled triangles) from
the R/V Thompson and R/V Knorr. Rms differences are calculated for 0.5 m s-1
bins of the vessel's speed over the ground using the absolute value of the wind direction
differences (i.e., range 0-180°). The number of values in each bin (open squares) are
presented in units of thousands.

Fig. 5. Time series plots of (a) heading-estimated (red) vs. meteorological true (black) wind direction and (b) vessel speed over the water (red) vs. the speed over the ground (black) from the R/V Knorr (02 November 1996). Note that the speed over the water drops out after 10:30 UTC due to an instrument malfunction.

Fig. A1. Platform-relative coordinate system with a zero reference angle,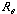 , not oriented to the bow.
, not oriented to the bow.

Fig. A2. Schematic representation of the vectors and angles involved in the true wind problem. See text for explanation of symbols.
Footnotes
1The American Practical Navigator is the primary resource
for navigational methods utilized by the United States Merchant Marine. Mariners
are trained using this text. The document was originally compiled by Nathaniel
Bowditch in 1802 and has been updated periodically by the United States Navy
Hydrographic Office since 1868.
 V) determined from one minute observations within a longer averaging period (six minutes in the following example):
V) determined from one minute observations within a longer averaging period (six minutes in the following example):
 v > 1.0 m s-1 (12 collocations with accelerations that are considered too rapid and prolonged) are flagged and removed, the mean difference changes to 0.55 m s-1, and the rms difference drops to 1.3 m s-1. These findings are consistent with an assessment of the NSCAT-1 model function in comparisons with the NDBC buoys by M. Freilich and R. S. Dunbar (1997, personal communication) and the TAO buoys by K. Kelly (1997, personal communication). The change in the mean is statistically significant, corresponding to 4.3 standard deviations of the mean. The almost 50% overestimation of the rms difference, prior to this quality control criterion, shows that there are applications where changes in the vessel's velocity can result is substantial averaging-related errors in the calculated true winds.
v > 1.0 m s-1 (12 collocations with accelerations that are considered too rapid and prolonged) are flagged and removed, the mean difference changes to 0.55 m s-1, and the rms difference drops to 1.3 m s-1. These findings are consistent with an assessment of the NSCAT-1 model function in comparisons with the NDBC buoys by M. Freilich and R. S. Dunbar (1997, personal communication) and the TAO buoys by K. Kelly (1997, personal communication). The change in the mean is statistically significant, corresponding to 4.3 standard deviations of the mean. The almost 50% overestimation of the rms difference, prior to this quality control criterion, shows that there are applications where changes in the vessel's velocity can result is substantial averaging-related errors in the calculated true winds.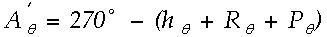
 designates an angle. The magnitude of A
is the same as the magnitude of P. Use of the heading instead of the
COG in (A1) is essential because the bow is rarely oriented in the direction of
ship motion over the fixed Earth. As an example, consider the bow of a ship is
oriented directly to the east (
designates an angle. The magnitude of A
is the same as the magnitude of P. Use of the heading instead of the
COG in (A1) is essential because the bow is rarely oriented in the direction of
ship motion over the fixed Earth. As an example, consider the bow of a ship is
oriented directly to the east ( = 90°). If there is either a strong current or wind from the north, then the vessel will be pushed to the south, resulting in a COG greater than 90°.
= 90°). If there is either a strong current or wind from the north, then the vessel will be pushed to the south, resulting in a COG greater than 90°.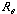 in Fig. A1) must be included in (A1) to correctly calculate the apparent wind direction.
in Fig. A1) must be included in (A1) to correctly calculate the apparent wind direction. ) in math coordinates is
) in math coordinates is 
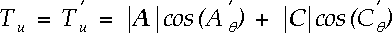
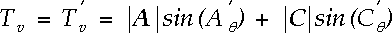
 T
T ) and direction (
) and direction ( ) can then be calculated:
) can then be calculated: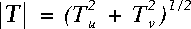
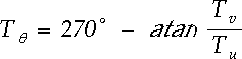
 to a direction from which the wind is blowing (meteorological convention) in the Earth coordinate system. For (A5) to return a correct angle, the atan function must have a range from -180° to 180° to determine the vector's trigonometric quadrant (e.g., the FORTRAN atan2 function). Also, any program using (A5) must have a check to avoid dividing by zero.
to a direction from which the wind is blowing (meteorological convention) in the Earth coordinate system. For (A5) to return a correct angle, the atan function must have a range from -180° to 180° to determine the vector's trigonometric quadrant (e.g., the FORTRAN atan2 function). Also, any program using (A5) must have a check to avoid dividing by zero. ) of 30.0° and a COG (
) of 30.0° and a COG ( ) of 45.0° both referenced to true north (0° in
a fixed Earth reference frame). The vessel is travelling at a SOG (
) of 45.0° both referenced to true north (0° in
a fixed Earth reference frame). The vessel is travelling at a SOG ( C
C ) of 5.0 m
s-1. The platform-relative wind, with the bow as the zero reference angle (
) of 5.0 m
s-1. The platform-relative wind, with the bow as the zero reference angle (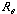 = 0.0°), is blowing from a direction (
= 0.0°), is blowing from a direction ( ) of 250.0° with a magnitude (
) of 250.0° with a magnitude ( P
P ) of 10.0 m s-1. The
conversion to math coordinates using (A1) and (A2) results in
) of 10.0 m s-1. The
conversion to math coordinates using (A1) and (A2) results in  = 350.0° and
= 350.0° and  =
45.0°. Computing the true wind components using (A3a) and (A3b) gives a
Tu = 13.4 m s-1 and a Tv = 1.8 m s-1. The meteorological true wind speed from (A4) is 13.5 m s-1 and the true wind direction, (A5), is blowing from 262.3°.
=
45.0°. Computing the true wind components using (A3a) and (A3b) gives a
Tu = 13.4 m s-1 and a Tv = 1.8 m s-1. The meteorological true wind speed from (A4) is 13.5 m s-1 and the true wind direction, (A5), is blowing from 262.3°. ) the parameters needed for computing a meteorological true wind or an estimate of the true wind (heading or course missing).
) the parameters needed for computing a meteorological true wind or an estimate of the true wind (heading or course missing).










 ) = 0°. The table is divided into input (not shaded) and output (gray shaded) values. Note that both the apparent and the true wind directions are referenced to true north, and all wind directions are angles from which the wind is blowing. Also the WMO convention is utilized for calm (direction = 0°) and north winds (direction = 360°).
) = 0°. The table is divided into input (not shaded) and output (gray shaded) values. Note that both the apparent and the true wind directions are referenced to true north, and all wind directions are angles from which the wind is blowing. Also the WMO convention is utilized for calm (direction = 0°) and north winds (direction = 360°). Oceanography
Oceanography Meteorology
Meteorology Merchant Marine (2)
Merchant Marine (2) Meteorology
Meteorology Oceanography
Oceanography Merchant Marine (2)
Merchant Marine (2)





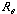 , not oriented to the bow.
, not oriented to the bow. 